Lorsque j’ai découvert ce qu’était une figure molle, j’ai radicalement changé mon point de vue sur l’utilisation d’un logiciel de géométrie dynamique par les élèves (Geogebra par exemple…). Finies les figures toutes faites, avec comme « seul » but la vérification que ça fonctionne bien comme le prof il a expliqué déjà 10 fois. Les élèves, au boulot ! À vous de découvrir et de comprendre les hypothèses des théorèmes !
Figure molle, figure robuste, c’est quoi cette histoire ?
Cet article de la revue MathémaTICE est incontournable. Mais lisez-le après avoir fini la lecture de ce billet… En gros, si l’on veut illustrer un théorème à l’aide d’un logiciel de géométrie, on a deux possibilités :
- soit la construction représente le théorème «en acte», les hypothèses sont toutes remplies, et on peut profiter du dynamisme pour vérifier que le théorème fonctionne bien : la construction est robuste, on travaille sur la thèse du théorème ;
- soit la construction représente le théorème pas tout à fait vérifié, il y a une hypothèse pas remplie, et c’est à l’élève de déterminer cette hypothèse en faisant en sorte que le théorème soit vérifié. La construction est molle, on travaille sur les hypothèses.
Peut-être que la conclusion de l’article cité ci-dessus, à propos des figures molles, sera plus claire :
Que le contrôle de l’élève porte sur une des hypothèses ou bien sur la conclusion, il y a une véritable incertitude chez l’élève au cours du déplacement, une marge de manoeuvre qui donne du sens au travail mathématique et à la conjecture émise. Et même si la validité de la conjecture ne fait aucun doute chez les élèves, cela ne nuit pas à la démarche de preuve. En effet, c’est le besoin de comprendre le pourquoi de la conjecture qui va les entraîner dans la recherche d’éléments de preuve. Ainsi, les situations « surprenantes », pour lesquelles la conjecture n’est pas évidente, favorisent l’entrée des élèves dans la preuve.
Pour terminer, quelques captures d’écran de constructions molles utilisées avec mes élèves :
Médiatrice comme lieu géométrique (n’oubliez pas le billet sur les lieux géométriques) :
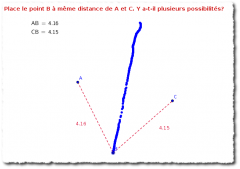
Cercle de Thalès :
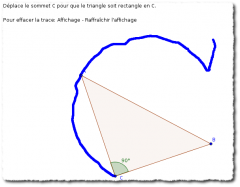
Somme des angles d’un triangle (billet sur la découverte de la somme des angles) :
