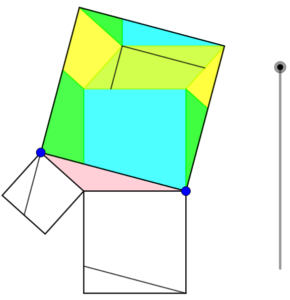
Mon éducation mathématique m’a plutôt fait voir le théorème de Pythagore comme quelque chose d’algébrique, une formule, trois lettres, une équation permettant de trouver la valeur d’un côté d’un triangle rectangle.
Mais ces derniers temps, je cherche à rendre les mathématiques plus tactiles, plus visuelles. Que ce soit dans l’étude des relatifs, des puissances, des formules d’aire ou des propriétés des quadrilatères (je présenterai bientôt l’utilisation de réglettes perforées…), du petit matériel tout simple permet de manipuler, toucher, expérimenter, et lier la connaissance à quelque chose de concret, ce qui manque parfois en mathématiques.
Après la découverte de Pythagore avec Geogebra, je propose ici deux ressources sur ce fameux théorème:
- un recueil de preuves géométriques, visuelles, illustrées avec Geogebra
- une de ces preuves imprimée en 3D (parce qu’on a la chance d’avoir une telle imprimante à l’école!)
Des démonstrations à n’en plus finir
Cette première ressource ne vient pas de moi, je l’ai glanée en fouillant sur geogebra.org. Elle s’intitule Pythagore sans mots. J’ai simplement laissé les élèves fouiller dans les démonstrations et repérer la façon dont le théorème est prouvé. Certaines sont plutôt classiques, on voit bien les trois carrés et l’égalité des aires, d’autres sont vraiment originales et procèdent par un découpage plutôt improbable…
Ne cliquez sur le lien vers le livret Geogebra que si vous avez du temps devant vous, parce que le risque d’addiction est grand! Il y a chaque fois un curseur ou un point à déplacer pour voir la preuve se faire sous nos yeux. C’est coloré et interactif, rien de tel pour crocher les élèves!
Et ce qui est génial, c’est que certaines preuves utilisent l’aire des carrés, mais d’autres des triangles, des pentagones, hexagones ou encoreplusgones :
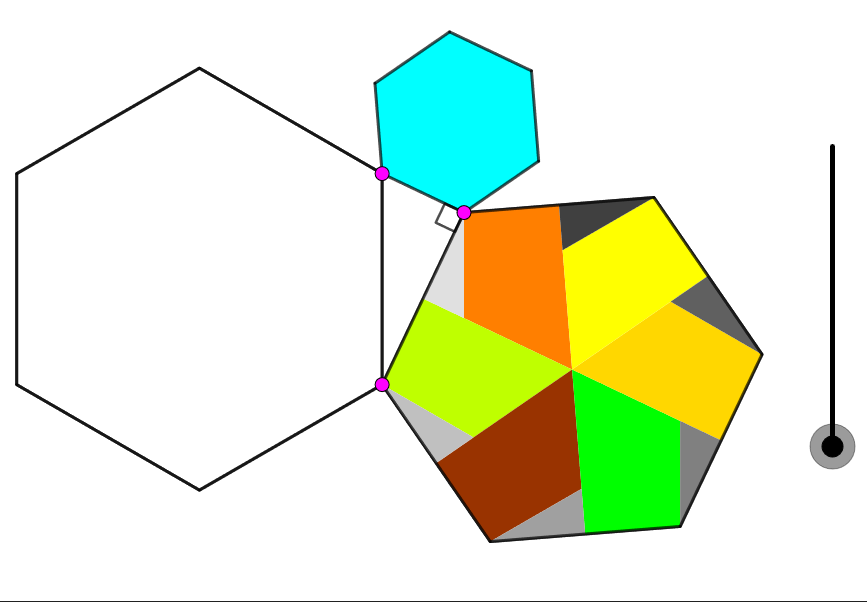
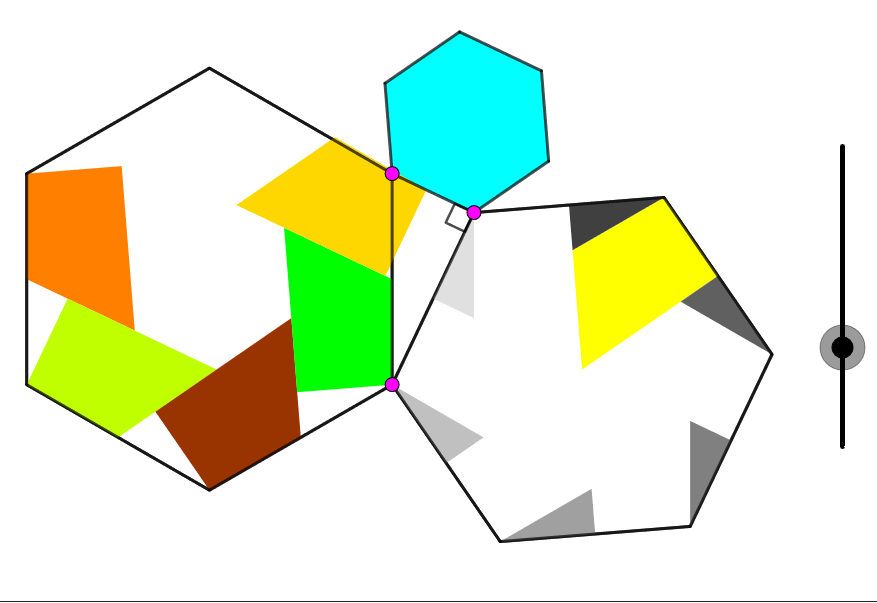
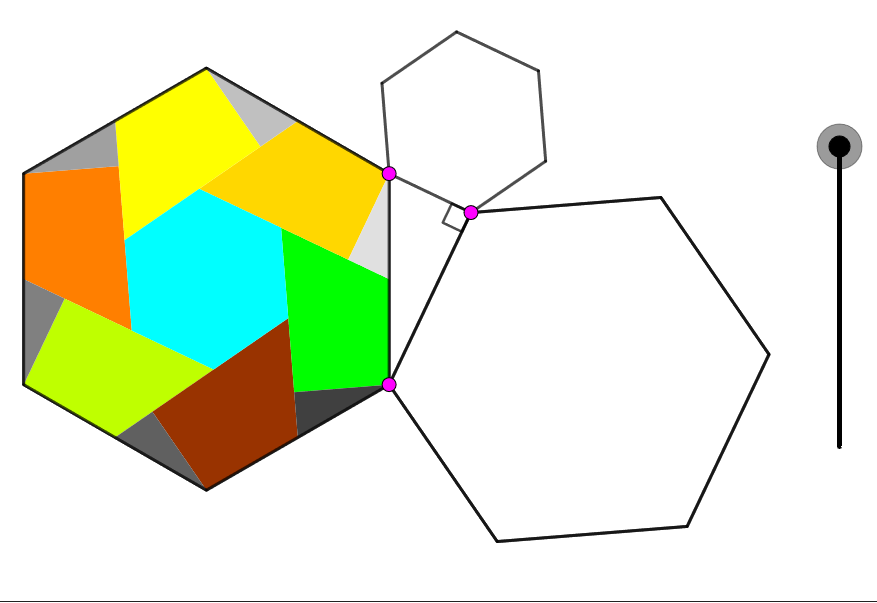
On y trouve aussi des preuves du théorème de Pythagore généralisé, nommé également loi des cosinus:
\(c^2 = a^2 + b^2 – 2ab \cos(\gamma)\)Une démonstration imprimée en 3D
Mais la preuve qui m’a titillé, c’est celle-ci (cliquer sur le lien pour accéder à l’animation) :
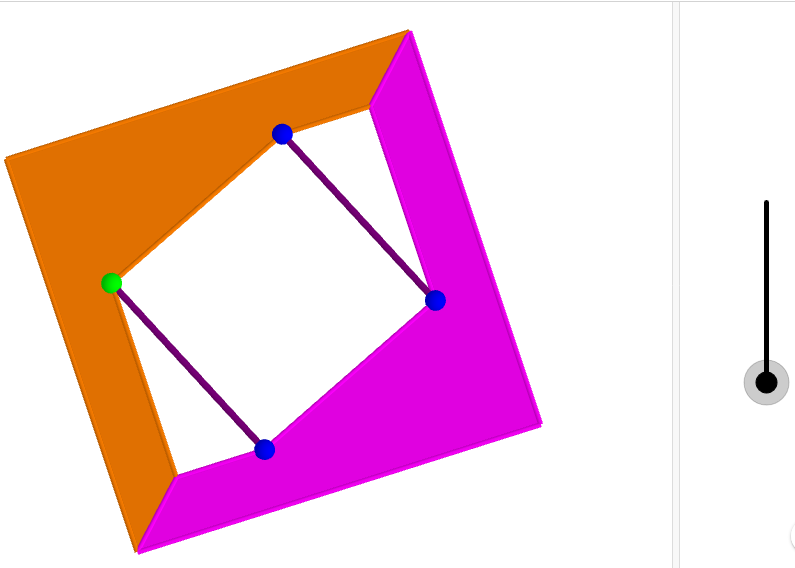
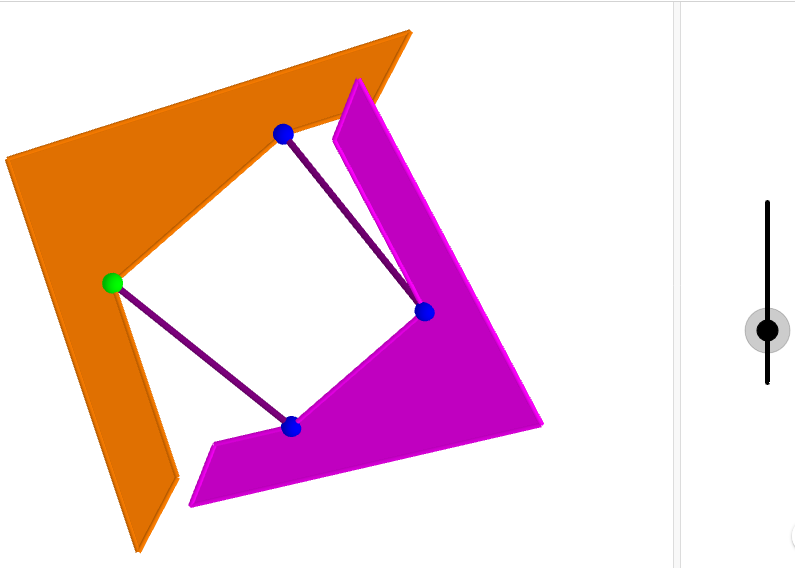
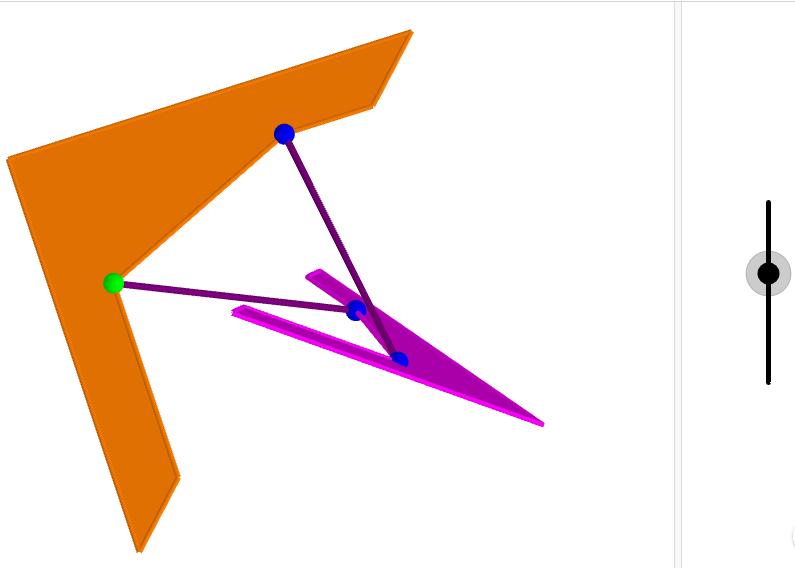
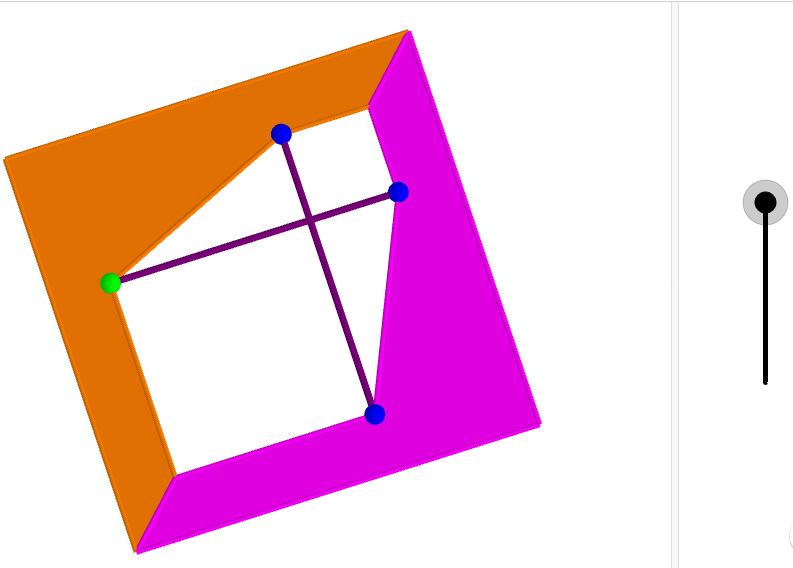
Comme toutes les autres preuves, elles se passe de mots. J’ai cependant testé avec un collègue, il n’a pas vu de lui-même. Mais bon, c’était un peu triché, je ne lui a pas dit qu’il fallait y voir Pythagore!
Sur Geogebra 3D, ça marche bien, on peut aussi faire pivoter les deux pièces dans l’espace. Avoir les deux pièces entre les doigts, c’est encore mieux! Deux bouts de plastique (ou de bois si quelqu’un est un peu manuel) et deux élastiques, et c’est l’apparition de Pythagore!
Ci-dessous les fichiers nécessaires à l’impression 3D:
- un SVG pour la forme de base (réalisé avec Inkscape) : preuve_pythagore.svg
- le dessin 3D (réalisé avec Tinkercad) : preuve_pythagore.stl
- le fichier prêt pour l’imprimante (réalisé avec Ultimaker Cura) : preuve_pythagore.gcode
L’objet pourrait aussi être découpé au laser, pour les heureux possesseurs d’une telle machine (ce qui n’est pas mon cas…).